1. 光学顕微鏡の基礎
1. 4 分解能と開口数
顕微鏡は物体を拡大して観察する装置なので、その性能を表す数値として倍率はもちろん大切ですが、物体の細部をきちんと識別できることの方がより重要です。この能力のことを分解能(Resolving power)といい、微小に接近している2点を識別できる最小の距離で表されます。この最小距離(解像限界)をδとすると、
で表されます。ここにkは係数で条件により異なりますが、一般に0.61又は0.5の値が使われます。λは使用する光の波長で、通常の可視光では0.55μm(最も目の感度が高い緑色の波長)となります。 またNAは開口数(Numerical aperture)で対物レンズの性能を決める上で最も重要な数値で、次の式で与えられます。
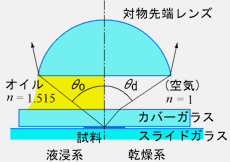
ここにn は物体側空間の媒質の屈折率、θは開口角といい軸上の1点から出て対物レンズに入る光のうち一番外側になる角度です(図1-6)。この式から、対物レンズの開口数が大きいほど分解能が高い(δが小さい)ことがわかります。乾燥対物レンズの場合、媒質は空気でn=1ですから、NAは1を超えることはなく、実際には0.95(θ=72°)が最大です。また対物レンズと試料(カバーガラス)との間を液体で浸す液浸対物レンズの場合、液浸オイルではn=1.515なので最大NAは1.45程度、水浸ではn=1.33なので最大NAは1.25程度となります。開口数が1.45の油浸対物レンズを使用して可視光観察を行う場合、分解能は(k=0.5とした場合)
となり、これが通常の光学顕微鏡の最小分解能ということになります。ただし前述のとおり、これはあくまでも2点分解能の値であり、微小物体の存在や動きに関してはこれよりはるかに小さい値のものが検出可能です(6章参照)。また高集積度LSI検査用として、遠紫外光(波長が可視光の半分程度)により分解能を大幅に向上させた対物レンズも製品化されてきています。
分解能は倍率とは直接関係ありませんので、拡大倍率だけを大きくしても分解能を超える微細構造は識別できません。適正な拡大倍率は対物レンズの開口数によって決まり、観察の場合400NA〜1000NAといわれています。分解能を超えて拡大することを無効倍率(馬鹿拡大)と呼んでいます。
顕微鏡で試料を観察した場合、試料の厚さ方向にピントが合う一定の範囲があります。これを(物 体側の)焦点深度(Depth of Focus:DOF)と呼び、次の式(ベレックBerekの式)で表されます。
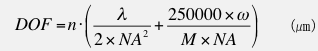
n : 標本と対物レンズとの間の媒質の屈折率 M : 総合倍率
ω:目の分解能(2分=0.00058)
この式の第1項は分解能から決まる深度で、第2項は観察者の目の分解能から決まる深度で個人差があります。
また顕微鏡の像の明るさは、光源の明るさに加え、開口数や総合倍率によって決まります。
